Introduction

Graphene has brought a lot of excitement to the scientific community since its isolation in 20041,2,3. Although the properties of twisted bilayer graphene (TBG) have been studied in the past decades4,5, recently it has become of great interest due to the finding of highly correlated phases such as superconductivity and Mott insulating phases when the twist angle is in the so-called magic-angle regime6,7. TBG is usually supported on top of a variety of substrates in the experiment. Interestingly, depending on the experimental setup, it can also be clamped between two layers of material. Among all of these, due to its atomically smooth surface that is relatively free of dangling bonds and charge traps8, hexagonal boron nitride (hBN) stands out due to the cleaner structures that can be fabricated. In fact, it has been shown that graphene mobility, when deposited on hBN8, is dramatically improved as compared to those on SiO2 substrates9. Furthermore, the large band gap of hBN has the advantage of having little interaction between the states of hBN and graphene that is opposite to the case with a metallic substrate where a large hybridization between the graphene and metal states can occur10.

Nevertheless, although the interaction between graphene and hBN is small due to the large band gap of hBN7, in the case of TBG on top of hBN, it has been shown that this small interaction can affect the electronic properties of TBG. Interestingly, the appearance of superconducting, insulating, and ferromagnetic phases in TBG supported on a nearly aligned hBN substrate has made this system even more appealing to study11,12,13,14. In the latter state, quantum anomalous Hall effect (QAH) has been measured and the material has been thought to be a Chern insulator13,14. Moreover, a ferroelectric phase has been found in Bernal-stacked bilayer graphene sandwiched between two hBN layers15. Therefore, the effect of the substrate supporting or embedding TBG could play a key role in the electronic properties of the system.

From a theoretical point of view, TBG has been studied using full or effective tight-binding (TB) models as well as continuum models due to the large number of atoms found in the moiré supercell16,17. On the other hand, due to the extra layer added when investigating the properties of TBG supported on hBN, the TB approach is hindered by the large number of atoms present in the supercell and most studies use continuum models. Regarding the effect of the structural relaxation on the electronic properties of the system, it is treated in a perturbative way, as well as is the case of the interaction of TBG with the substrate. Consequently, although in some works the relaxation of the lattices and the effect of the substrate are taken into account, the resulting model could be in some cases oversimplified and a more detailed calculation that takes into account a realistic relaxation and electronic structure is fundamental in order to explain certain experimental results, as well as to have a good starting point to obtain a good set of parameters for the continuum model18,19. Here, to achieve more realistic calculations we develop a full TB model for TBG where we also include the effect of hBN at an atomistic level. Moreover, to include the effect of the relaxation we perform semi-classical molecular dynamics in the systems that we study. Finally, we develop a continuum model that correctly describes the TB bands and that takes into account the relaxation effects as well as the effect of hBN.

Results

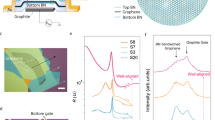
Typically, to perform measurements, TBG is supported or encapsulated with hBN. The supported case is a trilayer system composed of TBG lying on top of an hBN layer (TBG/hBN), as shown in Fig. 1a. The encapsulated case consists of a tetralayer system, where TBG is encapsulated by two layers of hBN (hBN/TBG/hBN), as shown in Fig. 3a. In the TBG/hBN case, we define the stacking geometry by starting from a non-rotated AAA configuration, where the AA sites of TBG share the same in-plane position (x, y) = 0 with the nitrogen atoms of hBN and, moreover, the graphene and hBN bonds are parallel. We then rotate the hBN layer (hBNbot) and the top graphene layer (Gtop) around the origin while keeping fixed the middle graphene layer (Gbot). As schematically shown in Fig. 1a, the twist angles are given by θtbg for the angle between graphene layers and θbot for the angle between hBN and the lower graphene layer. In the tetralayer structure, Fig. 3a, the top hBN layer is rotated by an angle θtop with respect to Gbot. We clarify that all twist angles (unless specified) are measured with respect to Gbot. By encapsulating TBG with hBN, three coexisting moiré patterns arise: the first one is induced due to the relative orientation between the two graphene layers, and the second and third ones appear due to the lattice constant mismatch between hBN and its adjacent graphene layer20,21,22,23,24. To perform the TB calculations a commensurate structure is required. For the trilayer TBG/hBN structure, a commensuration is achieved when LTBG = qLhBN, with q an integer, LTBG the TBG moiré length and LhBN the moiré length of Gbot and hBNbot heterostructure (see Supplementary Note 1). For example, the structures with θbot = 0.53°, 1.59°, 2.65° in Fig. 1 have q = 1, 3, 5, respectively.

Fig. 1: Structural and electronic properties of TBG supported on hBN.
figure 1

a Schematics of the atomic configuration of TBG/hBN. b Top view of the atomic configuration of TBG/hBN. High-symmetry stacking regions of AAA, ABC, and ACB are marked by red, black, and purple circles. Carbon, boron, and nitrogen atoms are depicted in brown, green, and gray, respectively. c In-plane strain, u(r), in TBG/hBN with fixed θtbg = 1.05° and varying θbot. The in-plane displacements are visualized with white arrows; the color data denote the local value of the in-plane twist of the atoms with respect to their original position (Δθ = ∇ × u) with positive values corresponding to the counterclockwise rotation. The moiré supercell is outlined in black. d Band structure and density of states of TBG/hBN with θbot = 0.53°. The color bar denotes the band for each valley \(\langle {\hat{V}}_{z}\rangle\) with \(\langle {\hat{V}}_{z}\rangle \approx 1\) if a state belongs to valley K and \(\langle {\hat{V}}_{z}\rangle \approx -1\) if a state belongs to valley \(K^{\prime}\). e, f Band structure and density of states of TBG/hBN with θbot = 1.59° and θbot = 2.65°, respectively. g The deformation potential VD and h pseudo-magnetic field B = ∇ × A induced by lattice relaxations in the TBG/hBN with θbot = 0.53°. The vector field A(r) is visualized with red arrows in (h). The twist angle between bilayer graphene is fixed to θtbg = 1.05° in all cases.

Full size image

Scalar potential and pseudo-magnetic fields

The lattice deformation due to the relaxation gives rise to periodic scalar and gauge potentials within the moiré unit cell24,25,26,27,28,29,30. In particular, the structural deformation leads to an on-site (or deformation) potential proportional to the local compression/dilatation and a pseudo-vector potential proportional to the shear deformations31,32. All these effects can be accurately considered in the TB calculation at an atomistic level (see Eq. (9) in Methods). The deformation potential VD(Ri) of a carbon atom located at Ri, is given by33:

$${V}_{D}({{{{\bf{R}}}}}_{i})={g}_{1}\frac{S({{{{\bf{R}}}}}_{i})-{S}_{0}}{{S}_{0}},$$
(1)

where S(Ri) is an effective area around the ith carbon atom that is modulated by local deformations, \({S}_{0}=3\sqrt{3}{a}_{0}^{2}/4\) is the effective area in equilibrium, a0 is the carbon-carbon distance and g1 = 4 eV for graphene, which corresponds to the screened deformation potential34. In free-standing TBG, the deformation potential originates a periodic scalar on-site potential centered at the unit cell origin (see Supplementary Note 2)32. As shown in Fig. 1g, the presence of a substrate induces an irregular periodic deformation potential. This irregularity reveals the complexity of the periodic potentials induced by the hBN on TBG that are found to be completely different from those of a single graphene layer on an hBN substrate25. In our TB model, we have two contributions to the on-site energy: the first one is the energy difference between nitrogen and boron. This contribution gives rise to different adhesion energies in the graphene/hBN unit cell and breaks the \({{{{\mathcal{C}}}}}_{2}\) inversion symmetry. This term is the main source of the mass gap in the graphene/hBN heterostructures24,26,27,30. The second contribution is the deformation potential Eq. (1) that slightly modifies the band structure (see Supplementary Note 4). This potential induces small periodic local mass gaps due to the potential difference between neighboring sites33.

In addition to the periodic scalar potentials, the structural relaxation gives rise to a pseudo-vector potential A with components proportional to the shear deformation31,35. In real space, the components of the vector potential are given by:

$$\begin{array}{l}{A}_{x}=\frac{\sqrt{3}}{2}({t}_{1}-{t}_{2}),\\ {A}_{y}=\frac{1}{2}(2{t}_{3}-{t}_{1}-{t}_{2}),\end{array}$$
(2)

where ti = 1,2,3 are the first nearest-neighbors inter-atomic interactions in the deformed lattice. If the strain is not uniform (t1 ≠ t2 ≠ t3), the vector potential generates a pseudo-magnetic field as

$${{{\bf{B}}}}=\frac{c}{ev}(\nabla \times {{{\bf{A}}}}),$$
(3)

where v is the Fermi velocity of graphene and c = 1 is a numerical factor depending on the detailed model of chemical bonding. The effect of the pseudo-magnetic field is introduced into the TB Hamiltonian by modifying the distance-dependent hopping parameters. It is important to note that the pseudo-magnetic field that acts on electrons from the valley \(K^{\prime}\) is exactly opposite to that acts on electrons from the valley K. Therefore, time-reversal symmetry is preserved.

TBG supported hBN

Figure 1 shows the strain tensor, pseudo-magnetic field, deformation potentials, and the band structure for θtbg = 1.05° with different θbot. Some interesting features are in order: for a twist angle θbot = 0.53°, at the corners of the unit cell the atomic displacements in Gbot do not have a circular “vortex” shape as in TBG (see Supplementary Note 2)31,36,37, instead, they have a triangular-like shape. As shown in Fig. 1c, the displacements have a counterclockwise behavior at the corners (AAA) and clockwise displacement in the inner regions (ABC and ACB). The magnitude of the in-plane twist of the atoms with respect to their original position, Δθ, has different values within the moiré because the corresponding atomic binding energies are different. This is due to the different stackings found in each region24,26. Figure 1g displays the distribution of the deformation potential in real space. As we can see, in Gbot its maximum value is about 60 meV in the ABC region, and a minimum of −40 meV is found in the AAA region. Notice that in the ACB region the on-site energies are small, as in the AAA centers. This behavior is reminiscent of that of monolayer graphene on hBN26,38. In addition, these magnitudes are quite close to those of graphene on an hBN substrate33. In Gtop, the on-site potential is one order of magnitude smaller. Figure 1h shows the vector potential A (red arrows) and the pseudo-magnetic field (in color) induced in both Gbot and Gtop. The pseudo-magnetic field in Gbot has a complex shape similar to a ‘fidget spinner’, and is completely different from that of monolayer graphene on hBN24 or free-standing TBG32. The resulting non-uniform pseudo-magnetic field in Gbot has a maximum value of about 18 T (which is almost twice as in pristine TBG32). In Gtop, the pseudo-magnetic field is smaller with a maximum of 9 T. In recent studies, the effect that an hBN substrate has on TBG is introduced by means of an effective periodic potential acting only on the nearest graphene layer18,39,40,41 with parameters obtained from calculations of a graphene monolayer on hBN. Our results indicate that this approach is correct, however, a renormalized set of substrate parameters should be considered while describing the periodic potentials42. We will discuss this in the following sections.

By increasing θbot the effect of the hBN on the TBG band structure is reduced. Our results indicate that, for the considered stacking, the effect of the substrate survives even for angles near 3° (see Supplementary Note 3). Nevertheless, it should be pointed out that small variations in the value of θbot for angles below that threshold have a huge impact on the electronic properties of the system. As θbot increases, shown in Fig. 1c, the period of the moiré length between Gbot and hBNbot is reduced43. For example, for θbot = 1.59° we have q = 3 resulting in LTBG = 3LhBN. The effect on the band structure is shown in Fig. 1d–f. Narrow bands are separated by a gap resulting from the breaking of inversion symmetry (\({{{{\mathcal{C}}}}}_{2}\)). In the nearly aligned situation, θbot = 0.53°, the gap between the narrow bands is ~25–30 meV. As the twist angle of the substrate increases, the second moiré length is reduced and the effects of the periodic potentials are suppressed. Interestingly, for θbot = 2.65° the gap is nonzero (Fig. 1f). The persistence of the gap for angles far from alignment is due to the large value of the mass term resulting from relaxation effects and the large difference of on-site energies between graphene and hBN sites44,45. In addition, as shown in Fig. 1d, e, the density of states (DOS) for two different angles is quite similar. We expect to find similar DOS for a range of small values of θbot. The persistence of the band gap for a window of small angles and the isolated narrow bands may explain the presence of a QAH in interacting models46, and other non-trivial band topology effects found in TBG with a nearly aligned hBN substrate12,13,14. Our results are consistent with previous studies that argue that the QAH would only appear if one or both θbot and θtop are near alignment18.

On the other hand, in the trilayer system shown in Fig. 1a, we can tune both the graphene twist angle θtbg and the substrate θbot. By modifying the graphene twist angle θtbg while keeping fixed θbot, the band structure is also modified. Figure 2 shows the band structure for θbot ≈ 0.53° and different twist angles, θtbg = 1.05°, 1.12°, 1.21°, and 2.28°. Here, it is important to note that, in our model, the ‘magic’ angle is around θtbg ~ 1.21°. As it can be seen, at this particular angle, the substrate induces a finite gap of about 30 meV. If we decrease the TBG angle, the bands become wider, especially the valence bands. Furthermore, the gap between the valence and conduction bands becomes slightly larger. Contrastingly, by increasing the angle, we can see that for θtbg = 2.28°, the AA bilayer graphene band structure is recovered47,48. In this particular case, the presence of hBN has the effect of opening a small gap at the Dirac cones.

Fig. 2: Layer degeneracy breaking.
figure 2

Band structure (red solid lines) of TBG/hBN with θbot = 0.53° and varying θtbg. Black dashed lines are the band structures of the corresponding free-standing TBG at each θtbg.

Full size image

In free-standing TBG, the layer degree of freedom is disentangled from spin and valley, providing eight-fold degeneracy in the low energy states. In the unperturbed system, the Dirac points are at the same energy (dashed black lines in Fig. 2) and, at low energies, Dirac cones only interact with their analogous at opposite layers. The presence of the hBN substrate induces a mass gap. However, the hBN has a larger effect on Gbot than on Gtop and the gapped Dirac cones of Gtop and Gbot are no longer at the same energy. Since the K point corresponding to layer 1 is mapped to a \(K^{\prime}\) point of layer 2 in the opposite valley, a ‘splitting’ in each of the conduction and valence bands is obtained in the full TB model due to the energy difference. Therefore, this splitting is a breaking of the layer degeneracy because the hBN has a larger effect on Gbot. In fact, as we will show in the following section, by adding a second hBN layer on the top and for certain twist angles, the degeneracy is recovered. A similar phenomenon is obtained in TBG in a uniform electric field49,50. Next, to identify the bands corresponding to each valley we define a valley operator of the form51

$${\hat{V}}_{z}=\frac{i}{3\sqrt{3}}\mathop{\sum}\limits_{ < < i,j > > ,s}{\eta }_{ij}{\sigma }_{z}^{ij}{c}_{i,s}^{{\dagger} }{c}_{j,s},$$
(4)

where i, j denotes next-nearest-neighbor sites, ηij = ± 1 for clockwise or counterclockwise hopping, respectively and \({\sigma }_{z}^{ij}\) the Pauli matrix is associated with the sublattice degree of freedom. The expectation value of this operator ranges from +1 to −1, which corresponds to the K and \(K^{\prime}\) valley, respectively. Figure 1d displays the band structure where the band corresponding to each valley is identified by different colors.

TBG encapsulated between hBN

We now consider the case of TBG encapsulated between two layers of hBN. Depending on the orientation and twist angle of each hBN layer with respect to TBG, several configurations can be obtained. Similar to the trilayer case, our starting point is an AAAA stacking configuration at the unit cell origin. Additional configurations can be obtained by modifying the stacking, see for example Refs. 40,52. In Fig. 3a we show a structure with arbitrary θbot, θtop, and θtbg, where the graphene layers are depicted in red and blue and the hBN substrate in green and black. Furthermore, we also show the different stacking configurations that can be found at the high-symmetry points along the moiré superstructure. Due to the three different degrees of freedom available when building this system, there is a large number of different heterostructures that can be generated. Here we are going to focus on three different cases where we fix θtbg to 1.05° and modify both θbot and θtop. It is important to note that all the twist angles are measured with respect to Gbot. For example, in the case where θbot = θtop, the twist angle with respect to Gtop is \({\theta }_{top}^{\prime}=-0.5{3}^{\circ }\).

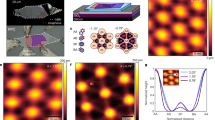
Fig. 3: Structural and electronic properties of TBG encapsulated between two hBN layers.
figure 3

a Schematic structure of the hBN/TBG/hBN system and the different high-symmetry stackings in the superlattice. Panels b–d from left to right display the band structure, in-plane twist of the atoms with respect to their original position, scalar potential, and pseudo-magnetic field. The twist angle of TBG is fixed to 1.05°.

Full size image

When θbot = θtop the lattice structure has hBNtop and hBNbot aligned with respect to each other. As shown in Fig. 3b, a large gap of about ~50 meV is found in the band structure. The corresponding pseudo-magnetic field has a three-lobed structure with a maximum magnitude of about 36 T, which is larger than in the trilayer case. The magnitude and direction of this field is opposite in each graphene layer and, as shown in the right panel of Fig. 3b–d is highly sensitive to the hBN twist angle. In the second column of Fig. 3b–d, we can see how the in-plane twist of the atoms with respect to their original position, Δθ, has a complex shape that also strongly depends on the hBN angle. Interestingly, in Gtop the in-plane strain field is oriented in the opposite direction with respect to the field in Gbot. The deformation potential is proportional to the change in the effective area around each atom with respect to its equilibrium position. As shown in the third column of Fig. 3b–d, the potential at the corners of the unit cell is negative and has a smaller absolute value than those in the interior regions, where there is a maximum. This behavior is reminiscent of monolayer graphene on hBN where it is known that the moiré pattern in the rigid system smoothly changes between AA type, AB type (carbon on boron), and BA type (carbon on nitrogen). Each of these configurations has different adhesion energy that is minimum at the AB stacking, while BA and AA are roughly similar24,26,28. The different energies create in-plane forces that tend to maximize the area of the AB regions and minimize the other regions. This behavior is completely captured by our results in the third column of Fig. 3b–d where in the red regions, the local area around each atomic site is maximized and the on-site potential is positive. Interestingly, this color difference allows us to distinguish the different stacking configurations between each TBG layer and its neighboring hBN layer by simply looking for the maximum or minimum in the corresponding deformation potential.

Interestingly, in the tetralayer structure hBN/TBG/hBN, for twist angles where θbot = θtop, Fig. 3b, the eight-fold degeneracy is recovered. As we will elucidate in the following section, this occurs because the periodic potentials acting in each graphene layer are opposite or with the same magnitude. On the contrary, if θbot ≠ θtop, as shown in Fig. 3c, the effect of the substrate is different in each graphene layer and the layer degeneracy is broken resulting in a band splitting. Notice that the pseudo-magnetic fields have different maximum values on each layer. The same happens for the in-plane strain. In principle, we can assume that the layer degeneracy is broken in structures with different θbot and θtop; however, this is not always the case. Fig. 3d shows the TBG band structure with different twist angles θbot and θtop where the layer degeneracy is recovered. By simple geometry we notice that the twist angle of hBNtop with respect to Gtop is θtop = 0.54° which means that each hBN layer is twisted in opposite directions with the same angle with respect to its nearest graphene layer and, therefore, the corresponding pseudo-magnetic and strain fields, Fig. 3d, have opposite directions and equal magnitudes. Our results suggest that the layer degeneracy breaking may be recovered if \(| {\theta }_{bot}| \approx | {\theta }_{top}^{\prime}|\). Interestingly, the DOS close to charge neutrality has a single peak. This indicates that even if θbot and θtop are small (or both hBN layers are nearly aligned with its corresponding graphene layer), the band structure can be modified completely. This can have important effects on experimental measurements. The strong dependence of the electronic properties of TBG for small values of θbot/top may explain why in some experiments the valley anomalous Hall conductivity in suspended or encapsulated structures of TBG with hBN is not always present12,13,53. In addition, our results indicate that adding a single hBN layer to TBG breaks the layer degeneracy giving rise to a splitting in the band structure. This effect will produce a double peak in the local DOS similar to the effect produced by a magnetic field32.

Effective continuum model for TBG on hBN

As we have seen previously, TB is a powerful tool to study the electronic properties of realistic TBG and related structures in combination with semi-classical relaxation methods. Nevertheless, another common approach is the derivation of a continuum model5 that describes the bands obtained from the TB calculations. This model could help us elucidate some of the obtained effects and explicitly explain the influence of the hBN substrate on the TBG. In fact, such substrate effect can be considered by including an additional effective periodic potential in the continuum model (see Eq. (13) in Methods).

Figure 4a shows the band structure obtained by fitting the parameters of the continuum model to our TB calculations for free-standing TBG (see Table 1 in Methods). As expected, our results clearly indicate that the continuum model parameters strongly depend on the twist angle. The addition of an hBN substrate to support a graphene monolayer breaks the inversion symmetry (\({{{{\mathcal{C}}}}}_{2}\)) of the crystal which results in gapped Dirac cones44,45,54,55,56,57,58,59,60,61,62,63,64. As mentioned before, by placing TBG on hBN, two coexisting moiré patterns arise: the first one is induced by the relative orientation between the two graphene layers, and the second one appears due to the lattice constant mismatch between hBN and the bottom graphene layer20,21,22,23,24. To qualitatively fit a continuum model to our TB results, we assume that the coexisting moiré patterns are identical. Previous studies18,39,40,41,52 have considered the effect of an hBN substrate on TBG by means of continuum models that use the parameters obtained by TB models of graphene on hBN20,21,22,23,24. Only in Ref. 40 a vertical relaxation within the continuum model is taken into account. To our knowledge, there are no previous works where a full TB model for TBG on hBN that takes into account lattice relaxations is used to fit such models. It is important to note that, although the fitting of the continuum model is qualitative, the full TB that we use is widely accepted and is in agreement with first-principles calculations as well as it has been used to support different experimental results32,65,66.

Fig. 4: Continuum model.
figure 4

Band structure of twisted bilayer graphene with θ = 1.05° calculated with TB (black lines) and continuum (red lines) model. a Free-standing TBG and b TBG/hBN.

Full size image
Table 1 Values for parameters of the continuum model of free-standing TBG obtained by the fitting model to the TB calculations.
Full size table

The effect of the substrate can be introduced as an effective potential acting on the adjacent graphene layer which is periodic in the moiré unit cell24,29:

$${V}_{SL}\left({{{\bf{r}}}}\right)={\omega }_{0}{\sigma }_{0}+{{\Delta }}{\sigma }_{3}+\mathop{\sum}\limits_{j}{V}_{SL}({{{{\bf{G}}}}}_{j}){e}^{i{{{{\bf{G}}}}}_{j}\cdot {{{\bf{r}}}}},$$
(5)

with amplitudes VSL(Gj) given by

$${V}_{SL}({{{{\bf{G}}}}}_{j})={V}_{s}({{{{\bf{G}}}}}_{j})+{V}_{{{\Delta }}}({{{{\bf{G}}}}}_{j})+{V}_{g}({{{{\bf{G}}}}}_{j}),$$
(6)

where

$$\begin{array}{l}{V}_{s}({{{{\bf{G}}}}}_{j})=\left[{V}_{s}^{e}+i{(-1)}^{j}{V}_{s}^{o}\right]{\sigma }_{0},\\ {V}_{{{\Delta }}}({{{{\bf{G}}}}}_{j})=\left[{V}_{{{\Delta }}}^{o}+i{(-1)}^{j}{V}_{{{\Delta }}}^{e}\right]{\sigma }_{3},\\ {V}_{g}({{{{\bf{G}}}}}_{j})=\left[{V}_{g}^{e}+i{(-1)}^{j}{V}_{g}^{o}\right]{M}_{j},\end{array}$$
(7)

with \({M}_{j}=(-i{\sigma }_{2}{G}_{j}^{x}+i{\sigma }_{1}{G}_{j}^{y})/| {{{{\bf{G}}}}}_{j}|\). The 2 × 2 Pauli matrices act on the sublattice index in a single graphene layer. Δ is a parameter that represents a spatially uniform mass term45. Notice that the potentials induced by the substrate, Eq. (5), preserve time-reversal symmetry. This allows us to describe its effect in a single-valley model. Surprisingly, having identified that some of the potential profiles in the TB solutions indicate the existence of additional harmonics (see Supplementary Note 7), we find that the modulation of VSL at smaller wavelengths has some effects on the narrow bands and, therefore, Eq. (6) has to be expanded up to two harmonics. As described in Ref. 24,29, the minimal model for an hBN substrate depends on eight parameters: uniform on-site term ω0, constant mass gap Δ, position-dependent scalar terms \({V}_{s}^{e}\) and \({V}_{s}^{o}\) that are even and odd under spatial inversion, respectively. Two position-dependent mass terms, \({V}_{{{\Delta }}}^{o}(e)\) and two gauge terms \({V}_{g}^{o}(e)\), odd and even respectively. In the case of the second harmonic, six additional periodic potential parameters are required. Therefore, the Hamiltonian of TBG/hBN depends on several parameters, four for TBG (Eq. (13) and Table 1 in Methods) and eight for the substrate, Eq. (5). The exact values and their dependence on the twist angles are known for single-layer graphene on hBN25 but they are still unknown for the combined system TBG/hBN or hBN/TBG/hBN. Obtaining exact values for a large set of parameters is a difficult task since several combinations can give similar results and a complete fitting is out of the scope of this work. Some qualitative estimations of the substrate parameters can be given by analyzing the band structures and the periodic potentials in Fig. 1. For the considered stacking in Fig. 1a, an estimated set of parameters is given by (in meV)

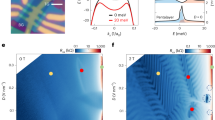
$$({w}_{0},{{\Delta }},{V}_{1,s}^{e},{V}_{1,s}^{o},{V}_{1,{{\Delta }}}^{e},{V}_{1,{{\Delta }}}^{o},{V}_{1,g}^{e},{V}_{1,g}^{o})=(3.0,31.62,-0.75,0.68,-0.02,3.4,-5.14,18.6)$$
(8)

for the first harmonic amplitudes and the only nonzero amplitudes for the second harmonic are the gauge fields \(({V}_{2,g}^{e},{V}_{2,g}^{o})=(-5.14,-9.3)\) meV. Figure 4b shows the band structure with the full TB model (black line) and the fitting with a continuum model (red line) using our estimated set of parameters which agree qualitatively with the TB calculations (see Supplementary Note 8). In particular, in order to achieve this kind of agreement, we found that: (i) the mass gap is large and (ii) the gauge terms require up to two harmonics. The first feature is in agreement with Ref. 40, where the band structure with a similar stacking has a large mass gap. As shown in Fig. 1, as θbot increases, the corresponding moiré length is reduced. This strongly suppresses the effect of the periodic potentials induced by the hBN and only the constant mass terms survives for large angles. As a final note, the strong gauge field in (ii) results from the effects of the relaxation of the trilayer system (TBG/hBN).

By fitting the continuum model to the TB band structures we have found that the dominant terms are the gauge fields which give rise to a pseudo-magnetic field and the mass term which is responsible for the large gap. By considering only the effects of the mass term (a similar analysis can be performed with the gauge potential) in Fig. 5 we show the band structure of TBG in both valleys (distinguished by color). We define Δb and Δt as the mass terms acting in Gbot and Gtop respectively. Figure 5a, d clearly shows the band splitting due to the different mass acting on each graphene layer. On the contrary, Fig. 5b, c are still degenerated due to the fact that the mass terms for the bottom and top layers are the same. This explains why in some of our TB results the presence of two hBN layers does not split the narrow bands. Our results indicate that in an experimental setup, if a hBN layer is nearly aligned with its closest graphene layer, the layer degeneracy is broken, which may result in a double peak in the local DOS, similar to the effect produced by a magnetic field32. We would like to recall that, in the encapsulated case, depending on the orientation of the hBN layers the degeneracy can be recovered.

Fig. 5: The effective mass term.
figure 5

Band structure of pristine TBG with different mass terms. a Δb = 30 meV and Δt = 0, b Δb = Δt = 30 meV, c Δb = −Δt = 30 meV and d Δb = 30 meV and Δt = −40 meV. In each panel, blue and red lines are the bands corresponding to each valley. The periodic potentials are set to zero.

Full size image

Discussion

In this work, we have studied the electronic properties of TBG supported on or encapsulated in hBN via a combination of an atomistic real-space TB model and semi-classical molecular dynamics. This procedure allows us to have a good description of realistic structures that are measured in experiments. Using this approach, we have found that hBN affects the electronic properties of TBG even when the angle between TBG and hBN is far from alignment. When studying TBG supported on an hBN substrate, the band structure shows a gap that separates the flatbands which we ascribe to a mass gap induced by the hBN. Moreover, hBN induces pseudo-magnetic fields which, in combination with the mass terms break the layer degeneracy and splittings within the bands appear. Interestingly, when adding an extra hBN layer, that is, when the TBG is clamped between two hBN layers the gap between the flatbands still appears, although the degeneracy of the bands can be recovered for certain twist angles. Finally, we have also developed a continuum model that correctly describes the calculated TB electronic properties. In order to qualitatively repeat the TB results, the substrate-induced periodic potential has to be expanded up to two harmonics. These kinds of models are helpful to understand the underlying physics behind the main features of the TBG/hBN heterostructures. We would like to stress that, in order to describe realistic structures as the ones found in experimental devices, our approach of mixing semi-classical molecular dynamics with an atomistic TB model is nowadays a state-of-the-art calculation since first-principles calculations are far from feasible due to the large number of atoms found in these systems. Therefore, the explanation of phenomena appearing in TBG either supported on an hBN or embedded between two of those layers such as superconductivity, correlated insulators or the recently found ferroelectric phase might only be possible using an atomistic TB calculation or continuum models that describe the electronic properties of such systems accurately.

Methods

Atomic relaxation

After constructing a commensurate supercell, to investigate the effect of the hBN substrate on the electronic properties of the system, we fully (both in-plane and out-of-plane) relax the TBG while keeping the hBN layer fixed in a flat configuration to mimic a bulk or a few layers substrate. To do so, we use semi-classical molecular dynamics as implemented in LAMMPS67. For intralayer interactions in the graphene layers, we use the reactive empirical bond order potential68. For interlayer interactions between graphene layers, we use the registry-dependent Kolmogorov–Crespi (RDKC) potential developed for graphitic systems69. We use the same RDKC potential for the interlayer interaction between graphene and hBN layers. The interactions strength of C − B and C − N are 60% and 200% with respect to the original C − C interaction, respectively33. We assume that the relaxed structures keep the periodicity of the rigid cases.

Tight-binding model

To calculate the electronic properties we use a full TB model given by23:

$$\begin{array}{l}H=-\mathop{\sum}\limits_{i,j}t({{{{\bf{R}}}}}_{i}-{{{{\bf{R}}}}}_{j})\left|{{{{\bf{R}}}}}_{{{i}}}\right\rangle \left\langle {{{{\bf{R}}}}}_{{{j}}}\right|+\mathop{\sum}\limits_{i}\varepsilon ({{{{\bf{R}}}}}_{i})\left|{{{{\bf{R}}}}}_{{{i}}}\right\rangle \left\langle {{{{\bf{R}}}}}_{{{i}}}\right|\\\qquad\; +\mathop{\sum}\limits_{i}{V}_{D}({{{{\bf{R}}}}}_{i})\left|{{{{\bf{R}}}}}_{{{i}}}\right\rangle \left\langle {{{{\bf{R}}}}}_{{{i}}}\right|,\end{array}$$
(9)

where Ri and \(\left|{{{{\bf{R}}}}}_{{{i}}}\right\rangle\) represent the lattice position and atomic state at site i, respectively, t(Ri − Rj) is the transfer integral between sites i and j. The last two terms in the above equation take into account the on-site contributions, where ε(Ri) encodes the carbon, boron, and nitrogen on-site energies and VD(Ri) the deformation potential resulting from the structural relaxation33. In the Hamiltonian, we assume that εB = 3.34 eV and εN = −1.40 eV, for boron and nitrogen atoms, respectively, and εC = 0 for carbon atoms23. For the transfer integral, we simply adopt the common Slater–Koster-type function for any combination of atomic species23:

$$-t({{{\bf{R}}}})={V}_{pp\pi }\left[1-{\left(\frac{{{{\bf{R}}}}\cdot {{{{\bf{e}}}}}_{z}}{R}\right)}^{2}\right]+{V}_{pp\sigma }{\left(\frac{{{{\bf{R}}}}\cdot {{{{\bf{e}}}}}_{z}}{R}\right)}^{2},$$
(10)

with:

$${V}_{pp\pi }={V}_{pp\pi }^{0}{\rm{exp}}\left(-\frac{R-{a}_{0}}{{r}_{0}}\right),$$
(11)
$${V}_{pp\sigma }={V}_{pp\sigma }^{0}{\rm{exp}}\left(-\frac{R-{d}_{0}}{{r}_{0}}\right),$$
(12)

where ez is the unit vector perpendicular to the graphene plane, R = ∣R∣, \({a}_{0}\approx 0.142\) nm is the nearest-neighbor distance of graphene, and d0 is the interlayer distance. \({V}_{pp\pi }^{0}\) is the transfer integral between nearest-neighbor atoms of graphene and \({V}_{pp\sigma }^{0}\) is that of vertically located atoms on the neighboring layers. We take \({V}_{pp\pi }^{0}\approx -2.7\) eV, \({V}_{pp\sigma }^{0}\approx 0.48\) eV, which gives a magic angle of 1.21°. If we set \({V}_{pp\pi }^{0}\approx -2.8\) eV, \({V}_{pp\sigma }^{0}\approx 0.44\) eV, the magic angle will be 1.05°. We adopt the same Slater–Koster parameters for the interactions between graphene and hBN, and intralayer interactions of hBN23. r0 is the decay length of the transfer integral, and is chosen as r0 = 0.317a0  so that the next nearest intralayer coupling becomes \(0.1{V}_{pp\pi }^{0}\). We set the cutoff distance of this hopping function to 0.6 nm since for larger distances the value of hopping energy is small enough that it can be safely neglected. We directly diagonalize the Hamiltonian to get the band structure, and compute the DOS of this system using a TB propagation method, as described in Ref. 70.

Continuum model for free-standing TBG

We consider the case of pristine TBG, where we need to fit four parameters: the velocity term, vf, which is known that depends on the twist angle71,72,73,74, the interlayer coupling parameters, \(\{u,u^{\prime} \}\), which strongly depends on the relaxation, and an additional periodic scalar potential Vs. The low energy Hamiltonian of TBG is given by,

$$H=\left(\begin{array}{cc}H({{{{\bf{q}}}}}_{1,\zeta })+{V}_{{{{\rm{s}}}}}({{{\bf{r}}}})&U{({{{\bf{r}}}})}^{{\dagger} }\\ U({{{\bf{r}}}})&H({{{{\bf{q}}}}}_{2,\zeta })+{V}_{{{{\rm{s}}}}}(-{{{\bf{r}}}})\end{array}\right),$$
(13)

where ql,ζ = R(±θ/2)(q − Kl,ζ) with Kl,ξ the graphene Dirac cones and H(q) = −ζ(ℏvf/a)q ⋅ (σ1, σ2) is the Hamiltonian for monolayer graphene and ζ = ±1 is a valley index. In the above equation, U(r) is the interlayer coupling between graphene layers which is given by the Fourier expansion,

$$\begin{array}{l}U=\left(\begin{array}{cc}u&{u}^{\prime}\\ {u}^{\prime}&u\end{array}\right)+\left(\begin{array}{cc}u&{u}^{\prime}{\omega }^{-\zeta }\\ {u}^{\prime}{\omega }^{\zeta }&u\end{array}\right){e}^{i\zeta {{{{\bf{G}}}}}_{1}\cdot {{{\bf{r}}}}}+\\\qquad +\left(\begin{array}{cc}u&{u}^{\prime}{\omega }^{\zeta }\\ {u}^{\prime}{\omega }^{-\zeta }&u\end{array}\right){e}^{i\zeta ({{{{\bf{G}}}}}_{1}+{{{{\bf{G}}}}}_{2})\cdot {{{\bf{r}}}}},\end{array}$$
(14)

where ω = e2πi/3, with u and \({u}^{\prime}\) the amplitudes which take into account relaxation effects as described in Ref. 16,75,76. G1 and G2 are the reciprocal lattice vectors. We also introduce an even and periodic scalar potential,

$${V}_{s}\left({{{\bf{r}}}}\right)=-{V}_{0}\mathop{\sum }\limits_{j=1}^{6}{e}^{i{{{{\bf{G}}}}}_{j}\cdot {{{\bf{r}}}}},$$
(15)

with V0 a constant term and the sum running over the six nearest neighbors reciprocal lattice vectors (or fist star), this is {G1, G2, G3, −G1, −G2, −G3}, with G3 = −(G1 + G2). We found that, although the magnitude of V0 is small, it has to be included in order to correctly fit the continuum model to the TB results. This potential appears to increase with the twist angle, however, for large angles, it becomes negligible. This potential, which is even and periodic, slightly distorts the narrow bands in a similar way as a Hartree potential with a negative filling would77. We believe that this potential is related to the different atomic rearrangements at the AA, AB, and BA sites due to the relaxation74,78. In addition, it is important to note that, the induced periodic potentials and mass gap due to the presence of an hBN substrate dominate over V0(r) in Eq. (15).